lautet die Überschrift eines auf reitschuster.de erschienenen Artikels. Sie ist ein Zitat des Nobelpreisträgers Luc Montagnier. In einem Interview soll er Folgendes gesagt haben: "Sie sehen es in jedem Land, es ist überall das Gleiche: Auf die Kurve der Impfungen folgt die Kurve der Todesfälle.“.

Gemeint sind Corona-Todesfälle. Es wird also von Montagnier und auch im Reitschuster-Artikel die Hypothese aufgestellt, dass die Impfungen Covid-Erkrankungen auslösen würden und zu vermehrten Todesfällen führen würden.

Direkt auf das Zitat Montagniers folgen im Artikel diese Sätze: "Dies zeigt auch ein Youtube-Video anhand der Daten des Institute for Health Metrics and Evaluation an der University of Washington. Danach steigen die Todeszahlen in einer ganzen Reihe von Ländern – darunter Österreich, Argentinien, Belgien und Brasilien – nach der Impfung teils signifikant an, nachdem sie zuvor stetig zurückgingen."

Zuerst wird also behauptet, dass das erwähnte Video die Aussage Montagniers bestätigen würde. Und danach wird gleich wieder relativiert. Plötzlich ist es nur mehr in einer Reihe von Ländern der Fall, nicht in jedem, wie es in der Überschrift behauptet wird. Da drängt es sich doch geradezu auf, sich das Video genauer anzusehen.

Das Video

Zuerst einmal ist festzuhalten, dass der Begleittext zu diesem Video gar nicht behauptet, dass die Sterbezahlen mit den Impfzahlen in den Ländern korrelieren. Es soll lediglich den Verlauf der Zahl Corona-Toten im Zusammenhang mit dem Start der Corona-Impfungen darstellen.

Sehen wir uns also ein paar Grafiken in dem Video an. Die Grafiken der im Artikel erwähnten Länder Argentinien und Brasilien könnte man als Beleg für die Behauptung ansehen, da dort die Todeszahlen nach dem Impfstart steigen. Aber bereits das ebenfalls genannte Belgien zeigt einen erstaunlichen Verlauf:

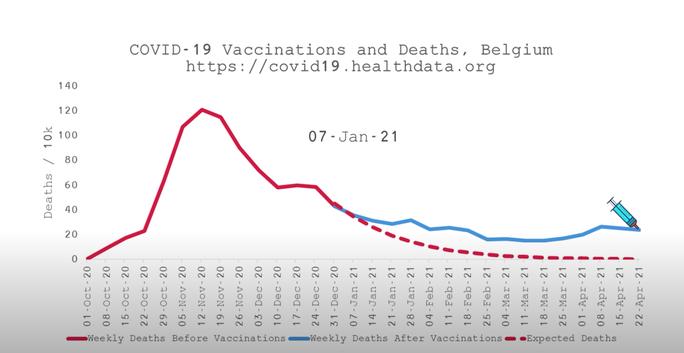
Screenshot https://www.youtube.com/watch?v=xSrc_s2Gqfw

Die rote Linie zeigt hier den Verlauf der Corona-Sterbezahlen vor dem Start der Impfungen, die blaue Linie den Verlauf nach dem Start der Impfungen, die rot gestrichelte Linie die "erwartete" Entwicklung der Sterbezahlen.

War da nicht die Rede von einem "signifikanten Anstieg" nach der Impfung? Ich weiß nicht, wer in der blauen Linie einen Anstieg nach dem Start der Impfungen erkennen kann. Ich jedenfalls nicht.

Auch die rot gestrichelte Linie der erwarteten Sterbezahlen ist rätselhaft. Was rechtfertigt diesen Verlauf? Warum soll das der erwartete Verlauf sein und der Verlauf der blauen Linie nicht? Für mich sieht auch die blaue Linie so aus, also ob sich der Verlauf der Zahlen "normal" weiter entwickelt.

Es gibt noch weitere interessante Grafiken in dem Video. Hier eine Auswahl:

Dänemark

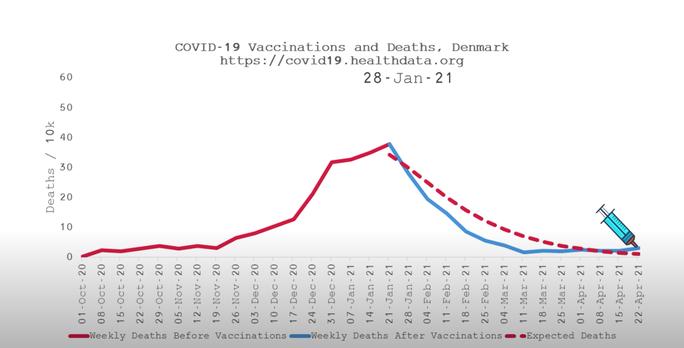
Screenshot https://www.youtube.com/watch?v=xSrc_s2Gqfw

Niederlande

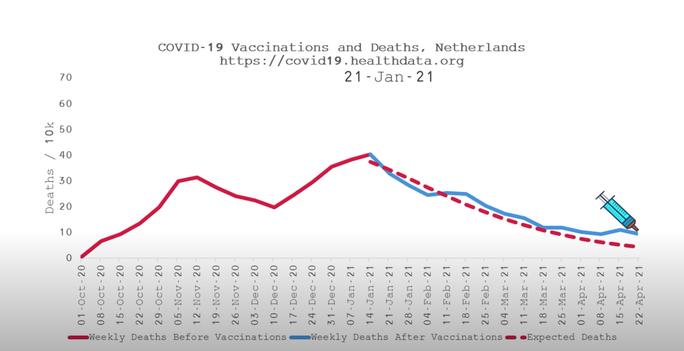
Screenshot https://www.youtube.com/watch?v=xSrc_s2Gqfw

Schweden

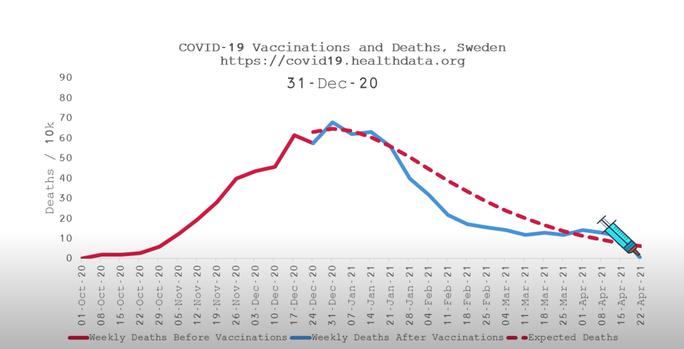
Screenshot https://www.youtube.com/watch?v=xSrc_s2Gqfw

Abgesehen davon, dass die "Prognose" hier meistens höher war als der tatsächliche Verlauf, wie kommt man auf die hier gezeigten Prognosen? Die rot gestrichelten Linien führen bei diesen Beispielen auf jeden Fall die Kurve nicht so weiter, wie man es rein anhand des Verlaufs davor vermuten würde.

Das wird leider in dem Video nicht erklärt. Es kann sein, dass die Prognosen auf Grund valider Modelle gemacht wurden. Oder die Kurven wurden einfach immer nach unten weitergeführt. Wir können es nur vermuten.

Es gibt noch ein paar Unschönheiten im Video. Zum Beispiel, dass die Y-Achse der Grafiken falsch beschriftet ist (es sind Tote pro Million, nicht pro 10.000) und die X-Achse anscheinend auch (das oben angegebene Datum stimmt nicht mit dem Impfstart im Diagramm überein). Das sind allerdings Kleinigkeiten, die die Aussage des Videos nicht verändern.

Aber was ist jetzt die Aussage des Videos? Wenn die Impfungen eine Erhöhung der Todeszahlen bewirken würden, was ja im Reitschuster-Artikel unterstellt wird, müsste das dann nicht ausnahmslos in jedem Land sichtbar sein? Wenn man eine Hypothese aufstellt und es ein einziges Gegenbeispiel gibt, ist die Hypothese widerlegt.

Die hier präsentierten Screenshots sind ausgesuchte Beispiele. Es gibt viele andere Länder, in denen die Sterbezahlen nach Impfbeginn tatsächlich ansteigen (wenn die im Video verwendeten Zahlen stimmen). Aber, wie gesagt, wenn die Impfungen eine Erhöhung der Sterberaten ursächlich bewirken würden, müsste es in jedem Land so sein.

Ist es aber nicht. Daher ist die Folgerung, dass dieses Video zeigen würde, dass die Todeskurve der Impfkurve folgt, nicht haltbar. Im Gegenteil, das Video ist ein starker Hinweis, dass es gerade nicht so ist.

Wo ist die Kurve?

Apropos "Kurve". Die Behauptung lautet ja, dass die Todeskurve der Impfkurve folgen würde. Aber wo ist die Impfkurve? Im gesamten Video wird keine Impfkurve gezeigt, nur der Zeitpunkt des Starts der Impfungen ist gekennzeichnet.

Also sehen wir zum Schluss anhand der Entwicklung in Österreich auch eine Impfkurve an. Im Video sieht die Grafik zu Österreich so aus:

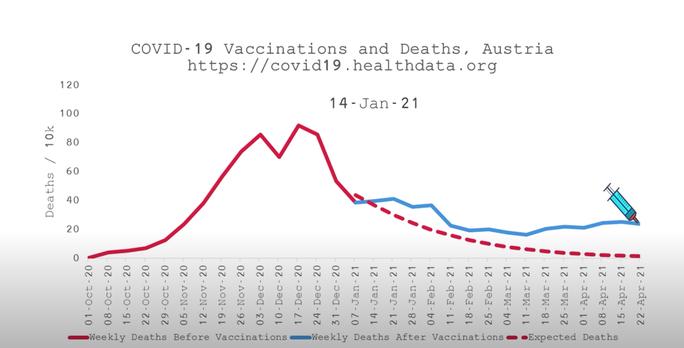
Screenshot https://www.youtube.com/watch?v=xSrc_s2Gqfw

Ich habe mir die Mühe gemacht und die benötigten Daten zusammengesucht, um selbst die Kurvenverläufe zu erstellen. Die Zahl der Covid-Toten habe ich von wikipedia, die verabreichten Impfdosen von raw.githubusercontent.com. Letzteres gibt die bekannte Website ourworldindata.org als Quelle ihrer Zahlen der verabreichten Impfdosen an.

Mit diesen Zahlen ergeben sich folgende Verläufe:

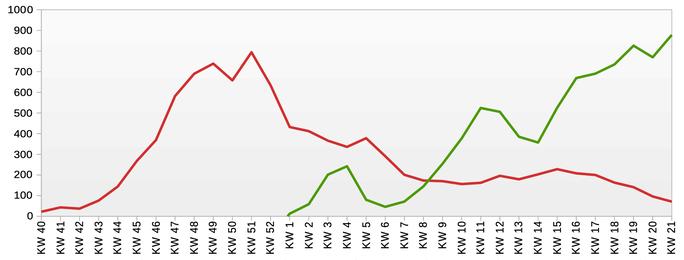
Dabei stellt die rote Kurve wie im Video die Zahl der Covid-Opfer dar, die grüne die Zahl der pro Woche erstmals geimpften Menschen, Zweitimpfungen werden nicht mehr gezählt. (1) (2)

Es ist deutlich ersichtlich, dass die Kurve der Todesfälle überhaupt nicht der Impfkurve folgt. Sie geht insgesamt klar in die andere Richtung.

Wenn also das Diagramm einen Zusammenhang zeigen kann, dann nur, dass bei steigenden Impfzahlen die Todeszahlen zurückgehen. Das belegt noch keinen kausalen Zusammenhang. Aber auch die ursprüngliche Argumentation beruht auf einer reinen Korrelation. Die Korrelation, die aus dem Diagramm abgelesen werden kann, ist aber genau die umgekehrte, die behauptet wird.

Es fällt noch auf, dass genau mit dem Impfstart die Geschwindigkeit des Rückgangs der Todesfälle abnimmt. Kann das mit der Impfung zusammenhängen?

Die untersuchte Hypothese lautet, dass die Impfung eine Corona-Erkrankung verursachen würde, an der die Menschen dann versterben. Da zwischen der Infektion und dem Tod bei Covid-19 im Durchschnitt aber etwa 2-3 Wochen vergehen, kann diese Verlangsamung nicht von der Impfung verursacht worden sein, da sie gleichzeitig mit dem Impfstart auftrat.

Auch der spätere Verlauf lässt sich mit der Hypothese nicht vereinbaren. Je mehr Menschen geimpft werden, umso weniger Covid-Tote gibt es. Das ist das Gegenteil dessen, was die Hypothese behauptet.

Fazit

Die Aussagen im Artikel auf reitschuster.de bezüglich des dort verlinkten Videos sind falsch. Das Video zeigt nicht und behauptet es auch nicht, dass die Covid-Todeskurven den Impfkurven folgen würden. Es zeigt nicht einmal Impfkurven.

Viel mehr ist es eine Widerlegung der behaupteten Aussage, da es eine Reihe von Ländern zeigt, in denen die Covid-Todeszahlen nach dem Impfstart sinken. Da die Impfkurven nach dem Impfstart zwangsläufig überall nach oben gehen, belegt das Video damit sogar ohne die Impfkurven zu zeigen, dass die aufgestellte Hypothese nicht stimmen kann.

Ich kann nicht beurteilen, wie die medizinischen Aussagen Luc Montagniers zu bewerten sind. Sollte er aber wirklich gesagt haben, dass die Todeskurven überall den Impfkurven folgen würden, hat er damit eindeutig unrecht.

---

(1) Die Kurve der Geimpften ist mit einem Faktor von 0,0025 multipliziert, um sie im gleichen Diagramm darstellen zu können. Die Skala auf der linken Seite gilt für die Todesfälle, um die absolute Zahl der geimpften Personen pro Woche zu erhalten, müssen diese Werte mit 400 multipliziert werden.

(2) Die rote Kurve der Covid-Todesfälle in meinem eigenen Diagramm verläuft nicht ganz gleich wie die im Video. Für meine Darstellung habe ich die Zahlen aus wikipedia verwendet, und zwar jeweils die Summe der jeweiligen Kalenderwochen. Welche Quelle die Macher des Videos verwendet haben oder wie die Daten bearbeitet wurden, weiß ich nicht. Es macht aber keinen großen Unterschied, der Verlauf unterscheidet sich nur im Detail, im Großen und Ganzen ist er sehr ähnlich.