Da ich mich wegen der Stochastikprüfung sehr viel mit Markovketten auseinandergesetzt habe, fiel mir dabei eines auf. Die Theorie der Kommunikationsklassen kann man auf das Thema Flirten usw. anwenden. Das wird bei manchen für ein großes ? sorgen, aber das ist mir egal. Ich habe das auf eine gewisse Dame angewendet, die offenbar im Kindergarten für Erwachsene ist. Das Ergebnis war der Beweis für die Richtigkeit "meines Satzes". Es handelte sich um eine Art von Kommunikation, die immer dann einseitig verlief, wenn es konkret wurde. Somit war es für mich unmöglich, den nächsten Schritt zu machen. Also verwendete ich "meinen Satz". Seine Voraussetzungen waren ja (leider) erfüllt.

Gleich vorweg: Frauen können diese Theorie auch auf Männer anwenden. Letztere verhält sich zwischen den beiden Geschlechtern sozusagen äquivalent. Also kann sie etwas frei übersetzt als "geschlechtliche Äquivalenzrelation" bezeichnet werden.

Ich hatte wiegesagt erst vor kurzem einen Fall, der mich eben auf "meine Theorie" brachte. Wenn Mann und Frau nicht in der gleichen Kommunikationsklasse (das Bett zählt hier nicht als Kommunikationsklasse... :-p) liegen, so wird daraus nichts. Das erkennt man dadurch, dass nur einer gibt bzw. nur von einem die Initiative kommt. Man kann das so interpretieren: Vom Mann führt ein "Weg" zur Frau, weil er ihr schreibt, sie anruft etc. Er "gibt" somit. Die Frau reagiert nicht, weshalb kein "Rückweg" existiert. Somit sind Mann und Frau zwei getrennte Kommunikationsklassen, die beide für sich selbst abgeschlossen sind (siehe unten).

Nun wollen wir genauer analysieren, wie Kommunikationsklassen funktionieren und aufgebaut sind. Im Beitragsfoto ist eine Markovkette zu sehen. Ich werde sie im weiteren Verlauf des Blogs auf deutsch "übersetzen". Um Kommunikationsklassen im Bereich Flirten erkennen zu können, muss man sie erst einmal allgemein verstehen.

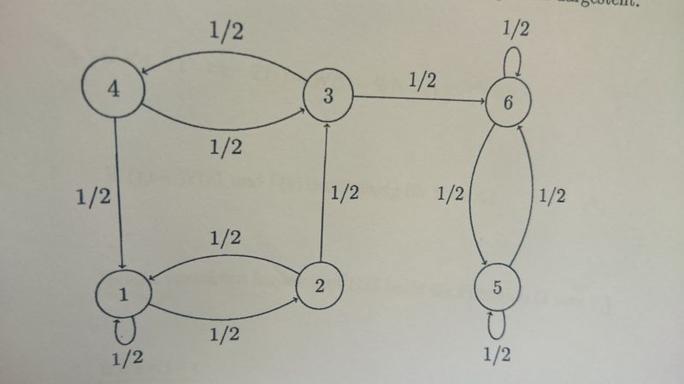
Eine Kommunikationsklasse besteht aus einem oder mehreren Zuständen. Diese "kommunzieren" eben miteinander (oder auch nicht). Seht euch nun das Blogbild genau an und lest die folgenden Zeilen. Ich beschreibe euch jetzt das Diagramm in Worten. Es gibt 6 Zustände, die alle irgendein Kommunikationsschema haben. Die Pfeile zeigen an, welche Zustände wie miteinander kommunizieren (je nachdem gibt es einseitige und beidseitige Kommunikation). Die Zahl daneben gibt die Wahrscheinlichkeit (WS) an, mit der ich von Zustand A in den Zustand B komme. Nun spielen wir dieses Schema für alle Zustände der Reihe nach durch.

1: Mit WS 1/2 bleibe ich dort. Bzw. komme ich mit WS 1/2 in den Zustand 2.

2: Mit WS 1/2 komme ich nach 1 zurück und mit WS 1/2 in den Zustand 3.

3: Mit jeweils WS 1/2 komme ich in den Zustand 4 bzw. 6 (:-p).

4: Mit jeweils WS 1/2 komme ich nach 3 zurück bzw. wieder nach 1.

5: Mit WS 1/2 bleibe ich dort und mit WS 1/2 komme ich nach 6.

6: Mit WS 1/2 bleibe ich dort und mit WS 1/2 komme ich nach 5.

1,2,3 und 4 kommunizieren miteinander, denn 1 -> 2 -> 3 -> 4 -> 1. Analog sieht die Kommunikation von 5 und 6 aus, denn: 6 -> 5 -> 6. Dabei spielt es keine Rolle, dass ich mit einer bestimmten WS in den Zuständen 1,5 und 6 verbleibe. Eine gewisse Restwahrscheinlichkeit bringt mich ja nach 2 bzw.nach 5 oder 6.

Schaut jetzt genau auf den Zustand 3. Ich komme zwar von 3 nach 6. Aber wenn ich einmal in 6 bin, bleibe ich entweder dort oder komme nach 5. Und von 5 wieder nach 6. Aber man gelangt nicht mehr in die Zustände 1-4 zurück. Somit hat man in dieser Markovkette 2 Kommunikationsklassen: #ÄÜ#1,2,3,4#ÜÄ# und #ÄÜ#5,6#ÜÄ#. Eine Kommunikationsklasse ist abgeschlossen, wenn man von ihr aus keinen Zustand erreicht, der nicht in ihr liegt. Demnach ist #ÄÜ#1,2,3,4#ÜÄ# nicht abgeschlossen, da ich von 3 nach 6 komme. #ÄÜ#5,6#ÜÄ# ist hingegen abgeschlossen, da ich von dort keinen der ersten 4 Zustände erreichen kann. Also wenn ich in 5 bzw. 6 bin, dann bleibe ich dort.

Eine Markovkette heißt irreduzibel, wenn sie nur aus einer Kommunkationsklasse besteht. Das kann puncto Flirten sowohl gut als auch schlecht sein. Entweder bin ich "meine eigene Kommunikationsklasse", weil die Frau nicht will. Oder "unsere Markovkette" bildet eine Kommunikationsklasse - demnach funkt es also zwischen uns.

Im Thema Flirten muss man sich den Mann bzw. die Frau jeweils als einen Zustand vorstellen. Nehmen wir dazu einfach die Zustände 5 und 6 aus dem Blogbild. Denkt euch stattdessen die Zustände "Mann" bzw. "Frau" und ignoriert den linken Teil des Fotos - also die Zustände 1-4 (der Pfeil von 3 nach 6 ist demnach auch weg). Mit einer bestimmten WS bleibt jeder alleine. Aber mit einer gewissen WS kommt der Mann zur Frau (bzw. umgekehrt). Letzteres heißt auf deutsch: Man trifft sich. Wenn die Kommunikation weiterhin funktioniert, dann kann das vielleicht zu einem ONS führen oder erstere ist gar die Grundlage für eine Beziehung.

Falls es aber so ist, dass sie nicht antwortet, dann kommuniziert jeder "Zustand" nur mit sich selbst. So bleiben beide (vorübergehend) 100%ig alleine und bilden somit verschiedene Kommunikationsklassen, die jeweils nur aus einem Zustand bestehen und beide für sich abgeschlossen sind. Wenn es allerdings schon funktioniert, dann bilden "Mann" und "Frau" eine Kommunikationsklasse #ÄÜ#M, F#ÜÄ#, die auch abgeschlossen ist (solange eben keiner fremdgeht).

Hat er z.B. eine andere, so ist die zuvor erwähnte Kommunkationsklasse nicht mehr abgeschlossen. Denn dann kommt man von ihm in einen anderen Zustand, der nicht in der eigentlichen Kommunikationsklasse liegt (es ist wohl sehr unwahrscheinlich, dass man von der "anderen" zur "eigentlichen Frau" zurückkommt... ;) ). Wenn "sie" das dann bemerkt, werden aus der einen Kommunikationsklasse #ÄÜ#M, F#ÜÄ# im schlimmsten Fall wieder die beiden (für sich abgeschlossenen) Kommunikationsklassen #ÄÜ#M#ÜÄ# und #ÄÜ#F#ÜÄ#. Lässt man "ihn" und "sie" die Rollen tauschen, funktioniert das analog.

Zum Schluss noch ein kleines Rätsel: FUF besteht im Wesentlichen aus zwei Kommunikationsklassen. Welche sind das? Bzw. sind diese abgeschlossen? Wer sich traut, darf mir die Lösung per PN schicken. ;)