Ich bilde mir ein eine recht nachhaltige Lösung für den Klimawandel gefunden zu haben, auch wenn diese vielleicht nicht ganz den Vorstellungen vieler Klimatologen entsprechen dürfte. Da es aber in der Wissenschaft nicht um Politik und vorgefasste Meinungen gehen darf, sondern in alle Richtungen zu denken geboten ist, sollte das kein Problem sein.

Ausgangspunkt meiner Überlegungen war, dass zumindest in den peripheren Regionen unseres Planeten das Meer als Wärmequelle dient. So ist es im norwegischen Stavanger mit durchschnittlich 5°C relativ mild, in sibirischen Jakutsk, das etwa auf dem selben Breitengrad liegt, mit -10°C ziemlich frostig. Auch wenn der Golfstrom hier mit reinspielen mag, gilt doch der Grundsatz: maritim: mild, kontinental: kalt.

Da die Ozeane und den gängigen Klimamodellen per se (also jenseits von El Nino, Wasserdampf usw.) keinerlei Rolle spielen, wollte ich mir die Strahlungseigenschaften von Wasser genauer ansehen. Denn immerhin dringt ja sehr viel Sonnenlicht durch die Oberfläche in das Wasser ein, wo diese Energie aber aufgrund der relativen Intransparenz gegenüber Infrarot nicht so leicht wieder entweichen kann. Sollte da nicht auch ein Treibhauseffekt entstehen?

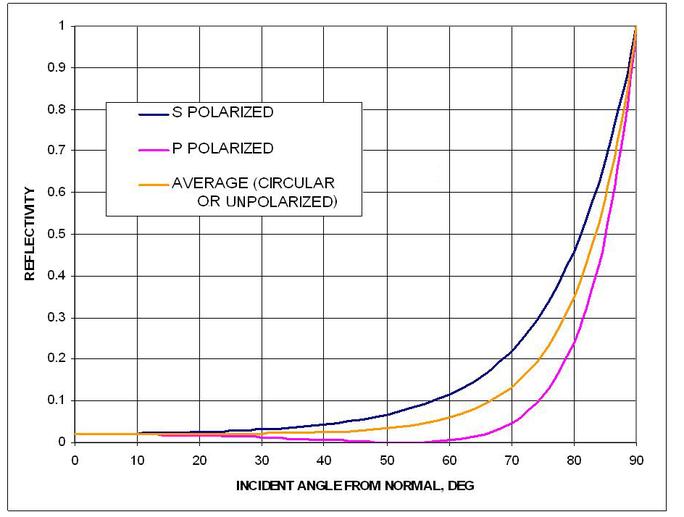
Zu Absorptions- und Emissionsgrad fand ich dann hoch interessante Informationen. Gleichsam wie die Reflexionsrate von Wasser bei niedrigem Winkel zunimmt, sinkt die Absorptionsrate zwangsläufig. Ein Phänomen das wir gut aus der Praxis kennen. So wird etwa bei einem Sonnenuntergang das Sonnenlicht sehr stark von einer (ruhigen) Wasseroberfläche gespiegelt. Gleichsam ist es schwer bis unmöglich Fische bei flachem Winkel zu sehen. Die Wasseroberfläche zeigt dann vor allem die Reflexion, und kaum die Emission von sichtbarem Licht, das Kirchhoffsche Gesetz lässt grüßen.

wikipedia

scienceofdoom.com

https://scienceofdoom.com/2010/12/27/emissivity-of-the-ocean/

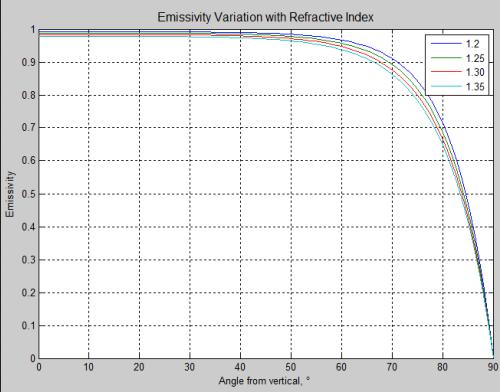
Wenn nun Emissions- und Absorptionsgrad bei gleicher Wellenlänge identisch sein müssen, so variieren doch beide wenn sich die Wellenlänge ändert. Überraschend ist daher, dass das Emissionsprofil im Bereich von Infrarot fast identisch mit jenem von sichtbarem Licht ist. Der oben verlinkte Blog diskutiert verschiedene Forschungsergebnisse zu diesem Thema. So ist zwar der Emissionsgrad eine Spur höher als der Absorptionsgrad, aber der Unterschied ist eben sehr gering.

Nun gilt es aber beide Funktionen entsprechend der Geometrie einer Hemisphäre zu gewichten und hier gibt es nun einen gravierenden Unterschied zwischen Absorption und Emission. Während jene Bereiche mit niedriger Absorptionsrate nur einen geringen Teil der gesamten Sonneneinstrahlung erhalten (sie verschwinden quasi schon am Horizont), der Bereich 80-90° wäre also nur mit 1-sin(80)^2 = 3% zu gewichten, tragen diese einen weit größeren Anteil an der hemisphärischen Emission. Der Bereich 80-90° wäre dann also mit cos(80) = 17,4% zu gewichten.

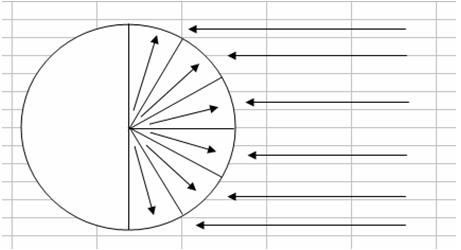
Leitwolf

Diese primitive Darstellung möge den Sachverhalt verdeutlichen, wäre aber natürlich in 3 Dimensionen zu denken.

Da mir keine mathematische Beschreibung obiger Funktionen zu Absorptions- und Emisssionsgrad vorliegen, habe ich eine synthetische Funktion hierzu generiert, die naturgemäß nicht perfekt sein kann, aber eine hinreichend präzise Annäherung darstellen sollte.

Leitwolf

Unter Verwendung dieser Funktion lässt sich nun eine Dichtefunktion für Absorption und Emission nach hemisphärischem Gradienten darstellen. Dies sieht dann etwa so aus:

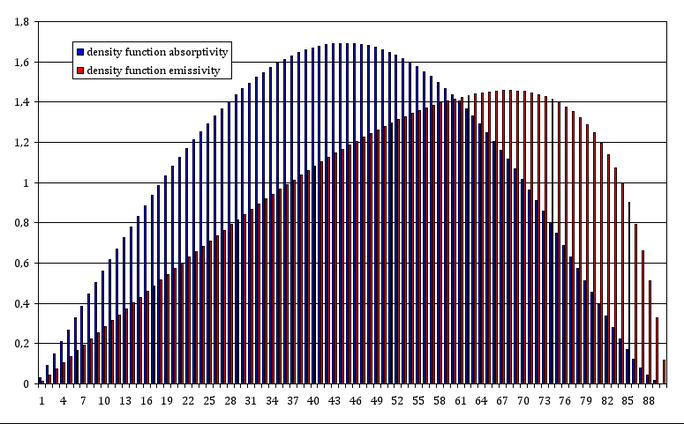
Leitwolf

Diese Vorgehensweise liefert mir nun die Werte 0,934 für die hemisphärische Absorption und 0,835 für die h. Emission. Nimmt man eine perfekten Schwarzkörper mit 280°K als Ausgangspunkt, so errechnet sich eine Temperatur von (0,934/0,835)^0,25 * 280 = 287,9°K. Eine gänzlich ozeanische Erde, ohne Atmosphäre, ohne Treibhauseffekt, sollte demnach also fast exakt so warm sein, wie die Erde in der Realität tatsächlich ist.

Nun stimmt diese Rechnung nicht ganz, da ich ein und dieselbe Funktion für E und A verwendet habe. Berücksichtigt man diesen kleinen Unterschied dann errechnet sich eine Temperatur die etwa einen Grad K. niedriger liegt. Allerdings ist auch der „cold skin“ Effekt nicht berücksichtigt, der dem wieder entgegen wirkt.

Dann kommt da noch etwas hinzu, was ich vor dem Hintergrund obiger Ausführungen wissen musste. Technisch war das etwas schwierig, aber es gelang mir am Ende dann doch. Ich wollte unbedingt abschätzen können wie sehr Wolken die nächtliche Abkühlung beeinflussen da man daraus ableiten könnte, wie stark der „Treibhauseffekt“ von Wolken in etwa sein dürfte.

Ich habe dazu Daten der NCDC verwendet und den ersten aufgefundenen brauchbaren Datensatz analysiert. Das waren in dem Fall die Wetterdaten von Parkersburg, WV des Jahres 2015. Wichtig war mir dabei, dass es a) keine Großstadt sein sollte, b) es hinreichend feucht wäre (weil sonst das Sample für bewölkte Nächte zu klein ausfiele), und c) auch Daten über Sonnenuntergang und Wolkenstatus verfügbar sind. Dann habe ich den Messwert der am nahesten am Sonnenuntergang lag zum Ausgangspunkt einer jeden Nacht gemacht und die relative Abweichung hiervon ermittelt.

Der Grad der Bewölkung wurde zu jedem Messzeitpunkt nach 5 Ausprägungen angegeben:

CLR .. clear sky

FEW .. few clouds

SCT .. scattered

BKN .. broken

OVC .. overcast

Ich wies diesen Ausprägungen dann jeweils einen Wert zwischen 1 und 5 zu (1 für CLR, 5 für OVC), und gab der jeweiligen Nacht den Durchschnitt aus diesen Werten. Dann gruppierte ich nach den Wertebereichen 1-2, 2-3, 3-4 und 4-5. Zusätzlich sind noch Bereiche 1-1,5 und 4,5-5 angegeben, wobei das Sample für letzteren mit 11 Nächten aber schon recht klein ist. Die x-Skala gibt übrigens die Zahl der Minuten x10 ab des ersten Messwertes an.

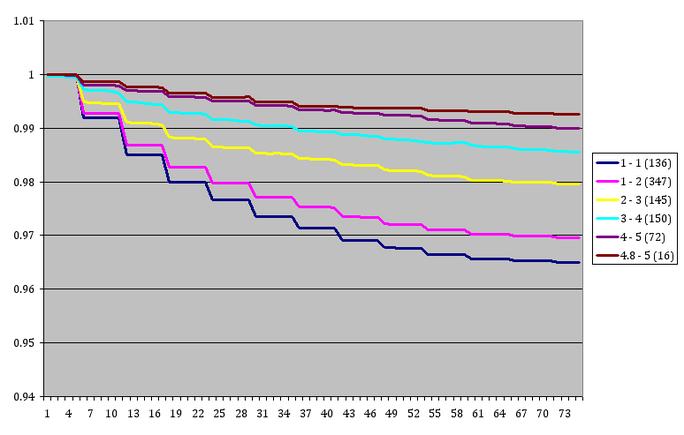
Leitwolf

Auch wenn ich erst nicht darauf hätte wetten wollen, funktioniert die Methode doch offenbar sehr gut. Wie zu erwarten korreliert die nächtliche Abkühlung sehr stark mit dem der Bewölkung. Umso klarer, desto schneller fallen die Temperaturen ab, umso bewölkter, desto konstanter bleiben sie.

Der Bereich 4-5 zeigt dabei eine Abkühlung die nur 20-30% jener ausmacht, die im Bereich 1-2 auftritt, wobei dieser Unterschied Anfangs eher bei 20% und später in der Nacht nur mehr etwa 30% beträgt. Das dürfte wohl daran liegen, dass zunächst die obersten Schichten des Bodens abkühlen und später erst tiefere Schichten entsprechend langsamer abkühlen, was also zu einer deutlichen Abflachung der Kurve bei klarem Himmel führt.

Dieses Ergebnis deutet nun also darauf hin, dass Wolken die nächtliche Abkühlung um mindestens 80% verlangsamen. Ein derartig hoher Grad an Remission von Infrarotstrahlung wäre aber auf der anderen Seite durch den Albedoeffekt von bzgl. Sonnenlichts kaum zu überbieten. Selbst wenn dieser bei dichter Bewölkung mit 90% angesetzt würde, ergäbe sich lediglich eine Relation von 90/80, sprich eine weitgehend klimaneutrale Rolle von Wolken. Wenn man nun aber noch bedenkt, dass die abgestrahlte Energiemenge von der Erdoberfläche größer angenommen wird, als die Strahlungsmenge die wir von erhalten (etwa 396 gegenüber 341), dann scheint es gar unmöglich, dass Wolken in Summe eine kühlenden Effekt hätten. Denn 80% von 396 sind mehr als 90% von 341.

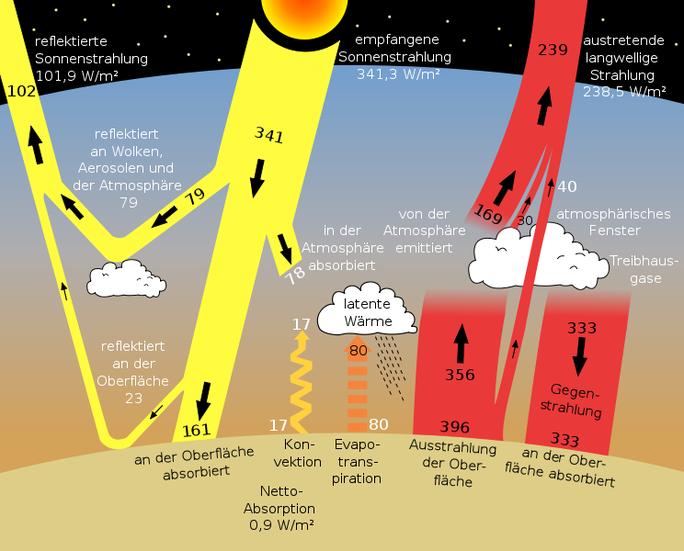
wikipedia

Nun halte ich diese Darstellung freilich für falsch, da der Emissionsgrad der Erdoberfläche eben nicht 1 ist. Dennoch müssen Wolken einen weitgehend neutralen Effekt auf das Klima haben, und nicht wie implizit (über den Albedoeffekt und den angeblich nur sehr geringen Treibhauseffekt von Wolken) unterstellt wird, einen massiv kühlenden.Effekt. Das bedeutet in weiterer Folge, dass Wolken in den gängigen Modellen eigentlich das wichtigste „Treibhausgas“ mit einem Anteil von gut 50% sein müssten.

Berücksichtigen wir aber nun die oben ausgeführten Strahlungseigenschaften von Wasser und addieren hierzu, dass Wolken netto auch keinen oder kaum einen kühlenden Effekt haben können, dann bleibt nebst Unschärfen, genau das Ergebnis stehen, das oben schon genannt wurde. Dann muss die Erdoberfläche in der Theorie rund 288°K warm sein. Was sie zufälliger Weise auch ist.

Nun muss ich mich wohl irren, denn wenn das so sein sollte, gäbe es ja nichtmal (abgesehen von Marginalien) einen Treibhauseffekt. Ich erkenne bloß meinen Fehler nicht.