POMMES LEIBOWITZ | Alle Welt spricht zur Zeit von Inzidenz, was irgendwie wissenschaftlich klingt. Aber was genau ist das eigentlich und wie wird sie berechnet? Hier zeige ich, wie völlig aussagefrei und manipulierbar diese als Wissenschaft getarnte Zahlenspielerei tatsächlich ist.

(c) RKI | mdr - Collage: Pommes Leibowitz

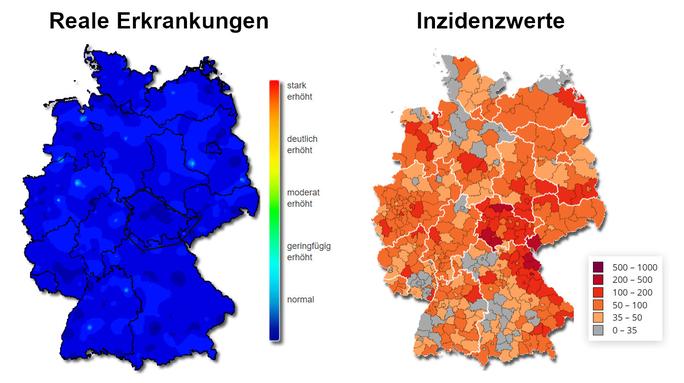
Die obige Grafik stellt links den aktuellen Stand respiratorischer Erkrankungen (Corona, Grippe, Lungenentzündung etc.) in Deutschland dar. Rechts werden die Inzidenzwerte nach Regionen dargestellt. Beides basiert auf Daten des RKI vom 27. Februar. In den Medien publiziert wird aber nur die zweite, auf Inzidenzen basierende Grafik. Zeit, sich mal Gedanken zu machen, was das überhaupt ist.

Wie wird die Inzidenz errechnet?

Die 7-Tage-Inzidenz, wie sie von Politik und RKI praktiziert wird, ist die Anzahl der an sieben aufeinanderfolgenden Tagen in einer Region gemeldeten positiven PCR-Tests pro 100.000 Einwohner. Noch mal genauer lesen: Nicht Neuinfektionen, wie die Medien als permanente Fake-News verbreiten - von Neuerkrankungen ganz zu schweigen - sondern schlicht positive Testergebnisse.

Die Tests können weder ermitteln, seit wann die Betreffenden infiziert sind, noch wird die komplette Bevölkerung getestet. Man führt einfach so viele Tests durch, wie man gerade Lust hat, und setzt dieses Ergebnis dann ins Verhältnis zur Bevölkerung, die im Gegensatz dazu eine feste Größe ist. Das heißt:

1. Je mehr Tests man durchführt, desto mehr positive Ergebnisse erhält man natürlich auch. Wenn einem der Inzidenzwert zu gering ist, muss man einfach nur die Anzahl Tests verdoppeln, und schon hat man den doppelten Inzidenzwert.

2. Wenn die Testdurchführung und -auswertung bereits an ihre Kapazitätsgrenzen stößt - die in jedem Land unterschiedlich sind - dann kann man immer noch den Inzidenz-Grenzwert herabsetzen, also den, der angeblich irgendeine Gefahr bedeutet. Frei Schnauze, nach dem Motto je niedriger desto besser.

Genauso gut könnte man allerdings auch das Sterben generell verbieten. Lasst uns eine Sterberate von Null anstreben. Das geht zwar nicht, aber man hat es immerhin versucht, und bei einigen Wählern kommt dieser Versuch womöglich gut an. Tatsächlich faseln einige "Experten" inzwischen von einer Inzidenz Null, was schon alleine an der Fehlerquote der Tests scheitert.

Wie ist das mit der Fehlerquote der Tests?

Da herrschen viele Missverständnisse, zumal es keine zuverlässigen Erkenntnisse zur Fehlerquote gibt. Die Herstellerangaben dürften mangels Testmöglichkeiten frei erfunden sein. Gehen wir für eine Beispielrechnung von einer Fehlerquote von 1 % aus. Was hat das konkret zur Folge:

Wenn tausend Tests durchgeführt werden, sind bei einer Fehlerquote von 1 % fünf Personen falsch positiv und fünf falsch negativ. Allerdings kann man ja nur falsch negativ sein, wenn man infiziert ist. Da nur ein Bruchteil der tausend Personen infiziert ist, schlagen also primär die fünf falsch Positiven zu Buche, während sich die Fehlerquote von 1 % bei nur einer Handvoll Infizierter kaum auswirkt.

Man spricht da auch von Grundrauschen. Es sind immer fünf falsch Positive dabei, die umso stärker ins Gewicht fallen, je geringer die Anzahl der tatsächlich Infizierten ist. So, wie das Rauschen in der Musik immer dann am auffälligsten ist, wenn die Musik leise ist.

Wie viele Infizierte gibt es nun auf 1000?

Eine Inzidenz von 50 (bereits unterschrittenes ursprüngliches Ziel) bedeutet 50 positive Tests auf 100.000 Bürger. Das sind 0,05 Prozent der Bevölkerung. Die Fehlerquote, die ein Grundrauschen von 0,5 Prozent falsch Positiven erzeugt, liegt also bereits um das 10fache darüber. Würde man tatsächlich alle 100.000 Bürger testen, hätte man eine auf der Fehlerquote basierende Inzidenz von 500. Die Tests sind also nicht nur völlig aussagefrei, da zufällig nach Gutdünken ausgeführt, sie produzieren außerdem primär falsch Positive.

Zum völligen Unfug exponentieller Hochrechnungen (zumal auf fehlinterpretierten Daten beruhend) hatte ich mich ja schon ausgelassen:

https://www.fischundfleisch.com/pommes/der-unsinn-mit-den-exponentiellen-hochrechnungen-70480