Fassung vom 07.12., 06:40 Uhr

Aufgrund der Kommentare habe ich den Artikel überarbeitet, um die Manipulationen stärker herauszustellen.

Auf dem Titelbild eines Servus-Beitrages liest man folgendes: "03.Dez | 3:28 Min | Seit Beginn der Pandemie sind insgesamt rund 3.500 Menschen an oder mit einer Corona-Infektion gestorben. Am Donnerstag melden die Behörden 92 Todesfälle. Mitte November gab es so viele Todesfälle wie seit Jahrzehnten nicht. Aber nur auf den ersten Blick. Denn: Die Bevölkerung ist in den vergangenen Jahren nicht nur gewachsen, sie ist auch älter geworden." Zitat Ende.

Schauen wir uns erstmal kurz die nackten "Raw Data" der wöchentlichen Todeszahlen an, um die es geht:

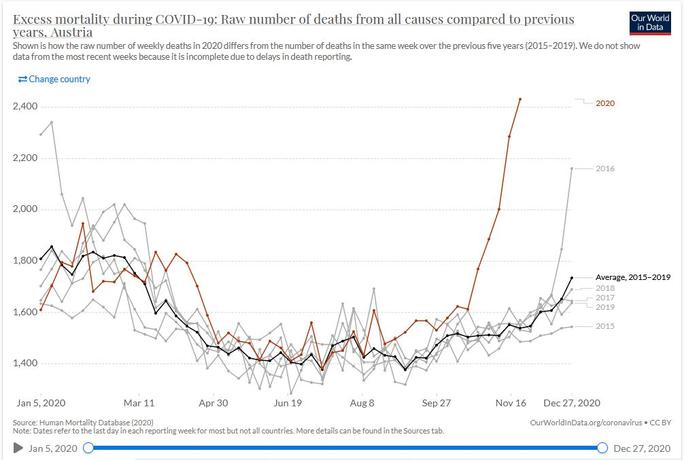
Our World In Data

Die schwarze Kurve zeigt die wöchentlichen Toten im Mittel der Jahre 2015 bis 2019. Die rote Kurve für 2020 geht seit 25.10. steil nach oben und steigt am 22.11. auf 2.431 - trauriger Rekord im Zeitraum seit mindestens 2015.

Am Morgen des Sendetages (03.11.) des Servus-Beitrages waren die vollständigen Daten der roten Kurve bereits bei Statistik Austria veröffentlicht, und der ORF hatte um 9:36 Uhr schon einen ausführlichen Artikel online:

ORF https://orf.at/stories/3192236/

Zurück zu Servus-TV: Das Video vom 03.12. ist in Deutschland nicht (mehr?) online, aber ein Screenshot zeigt, was die Redakteure für die Nachrichten aus den besagten (und weiteren) Daten gemacht haben:

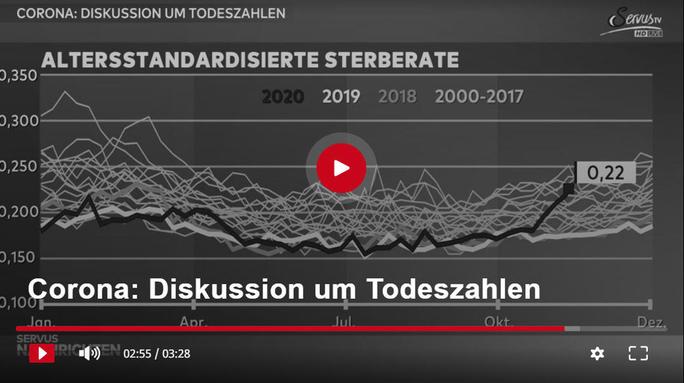
Servus-TV

Im Verlauf der schwarzen Kurve für 2020 erkennt man die rote Kurve von Our World in Data wieder. Eine Analyse der 2020er Kurve mit dem altersstandardisierten Endwert 0,22 ergibt, daß sie nur die Daten bis zur 45. Kalenderwoche bzw. 08.11. mit 2.001 Wochentoten zeigt.

Servus-TV arbeitete also mit Daten, die bei der Sendung bereits 2 Wochen lang veraltet waren. Die Zeitachse ist extrem grob skaliert, so daß man diesen Trick beim Anschauen eines 3,5-Minuten-Beitrages nicht erkennen kann.

Das Gekrissel oberhalb der dicken Kurven von 2018 bis 2020 sind insgesamt 18 (in Worten: Achtzehn!) altersstandardisierte Kurven, ab dem Jahr 2000.

Warum aber wählt man die komplizierte Altersstandardisierung, anstatt einfach die realen Todeszahlen ab 2000 zu zeigen?

Der Blick unter die letzten Kurven im Vergleich zur 1. Grafik von Our World in Data bringt die Antwort: Bei Our World in Data streuen die früheren Kurven munter über und unter die 2020er Kurve, aber bei Servus-TV ist der Bereich unterhalb der 2020er Kurve merkwürdig leer. Stattdessen tummeln sich die älteren Vergleichskurven allergrößtenteils oberhalb der dicken Kurven ab 2018.

Nun wird klar:

Bei der Altersstandardisierung werden mittels bevölkerungsstatistischer Umrechnungen die ältesten Todeskurven so weit über die 2020er Kurve gehoben, daß die Daten der 2.Coronawelle bis 08.11. noch im Streufeld der anderen 20 Kurven liegen.

So wird optisch suggeriert, daß die 2020er Todeszahlen nicht ungewöhnlich hoch wären. Mehr zum Hintergrund dieser Servus-Grafik findet Ihr hier.

Ergänzt man die Servus-Grafik mit den Daten vom 15. und 22.11. (die bei der Sendung bereits bekannt waren!) dann bricht die Illusion der Normalität der 2020er Todeszahlen zusammen:

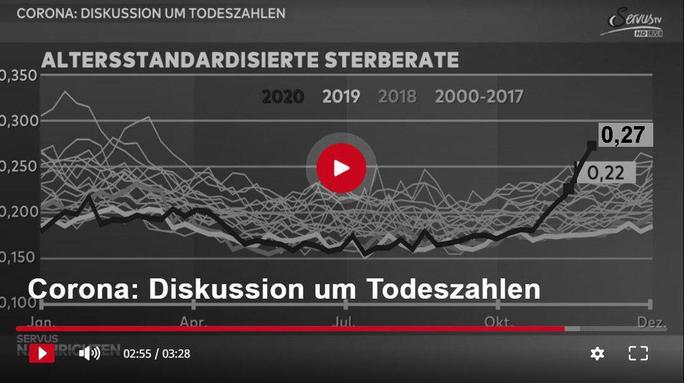
Servus TV + eigene Ergänzungen

In einem überaus freundlichen Kommentar wurden farbige Grafiken der gleichen Kurven verlinkt, die ebenfalls in der 45. Woche enden. Die beste von ihnen habe ich wieder auf die Woche 47 aktualisiert:

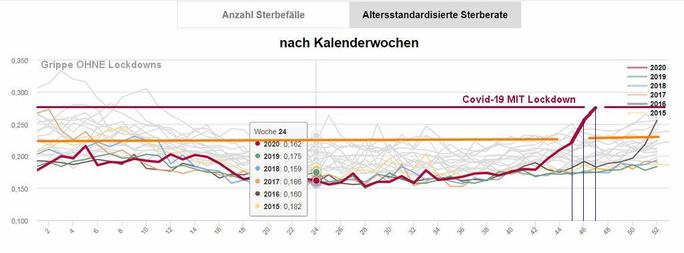
Statistik Austria?

Servus-TV verbreitete Daten, die nur bis zur orangen Querlinie reichten, obwohl schon die Daten der roten Querlinie bekannt waren.

Um auch diese herbstlichen(!) Wochentoten mit einem Kurvenstreufeld abzudecken, hätten die Manipulateure von Servus-TV noch weiter in Richtung 1900 zurück graben müssen.

Aber eine Jahreszahl aus dem letzten Jahrhundert im Kopf der Grafik (z.B. 1980 - 2017) wäre dann doch zu auffällig gewesen.

Die österreichischen Todesdaten nach dem 22.11. lassen sogar einen Peak der 2020er Kurve deutlich oberhalb von 0,3 erwarten . . . in ca. 2 Wochen wissen wir vielleicht mehr, je nachdem schnell oder langsam Statik Austria arbeitet.